No seriously what is Entropy

I always found the popular science description of entropy as ‘disorder’ as a bit unsatisfying.

It has a level of subjectivity that the other physical quantities don’t.  Temperature, for example, is easy- we all experience low and high temperatures, so can readily accept that there’s a number that quantifies it. It’s a similar story for things like pressure and energy. But no one ever said ‘ooh this coffee tastes very disordered.’

Yet entropy is in a way one of the most important concepts in physics. Among other things, this is because it’s attached to the famous second law of thermodynamics, with a significance towering over the other laws of thermodynamics (which are, in relation, boring as shit). It states that the entropy of a closed system can only increase over time.

But what does it all mean? What is entropy really? I intend below to give you a bit of a tour through the different angles on the concept of entropy. I go into a bit more detail than you would need maybe for a thermodynamics exam, but the extra detail is what makes entropy so damn cool and interesting.

I’ll start with the most general definition of entropy. Then, applying it to some everyday situations, we can gradually build up an idea of what physicists mean when they say ‘entropy’.

1: Shannon: Missing Information

Fundamentally, entropy is not so much the property of a physical system, but a property of our description of that system. It quantifies the difference between the amount of information stored in our description, and the total quantity of information in the system, i.e. the maximum information that could in principle be extracted via an experiment.

Usually in physics, it’s too difficult to model things mathematically without approximations. If you make approximations in your model/description, you can no longer make exact predictions of how the system will behave. You can no longer be certain about what will happen. However, you can instead work out the probabilities of various outcomes.

Let’s define some mathsy ideas about probabilities. Imagine some experiment with a number of possible outcomes, we call outcome 1, outcome 2, outcome 3 … We can assign to each of these outcomes a probability p₁,p₂,.. Each p is a number between 0 and 1. p=0 means it definitely won’t happen, p=1 means it definitely will, and p=0.5 means a 50/50 chance. You get the idea.

Surprise

A nice way to introduce entropy is to imagine how surprised you would be by the outcome of some experiment. Consider the simple example of flipping a coin. Your pal Barbara pulls out a coin to decide where to go for dinner or some shit like that. Before she flips the coin, you know that p_heads=0.5, and p_tails=0.5. She flips the coin and it comes up heads. You’ve gained a bit of information. Barbara wins and you go to bloody Nando’s again.

After a while of Barbara always winning whenever she tosses a coin to decide things, you start to suspect that she’s using an unfair, weighted coin. You have a new model of the coin: let’s say p_heads=0.9, and p_tails=0.1. Now, when she flips the coin again, and it comes up heads, you have gained less information than before. You already knew heads was likely. If it came up tails, you would have been surprised, that was less likely so you’ve gained more information.

Eventually, you discover that actually it’s one of these joke coins that is heads on both sides. So p_heads=1 and p_tails=0. If she flipped it again, and it came up heads, you would have gained no new information, no surprises, since you already knew for sure it would come up heads.

What we’ve seen in these scenarios are outcomes of varying level of surprise. The amount of surprise has been going in the opposite direction as the probability of the outcome that occurred. p=1 -> no surprise at all, p=0.9, not much surprise, p=0.5 -> a bit of surprise, p=0.1 -> lots of surprise. To quantify the information gained from an event with probability p, we need a function of p that becomes zero when p=1, and grows as p decreases. With this in mind, the best way to mathematically quantify information is this: the information gain of observing an outcome with initial probability p, is given by minus the logarithm of p.

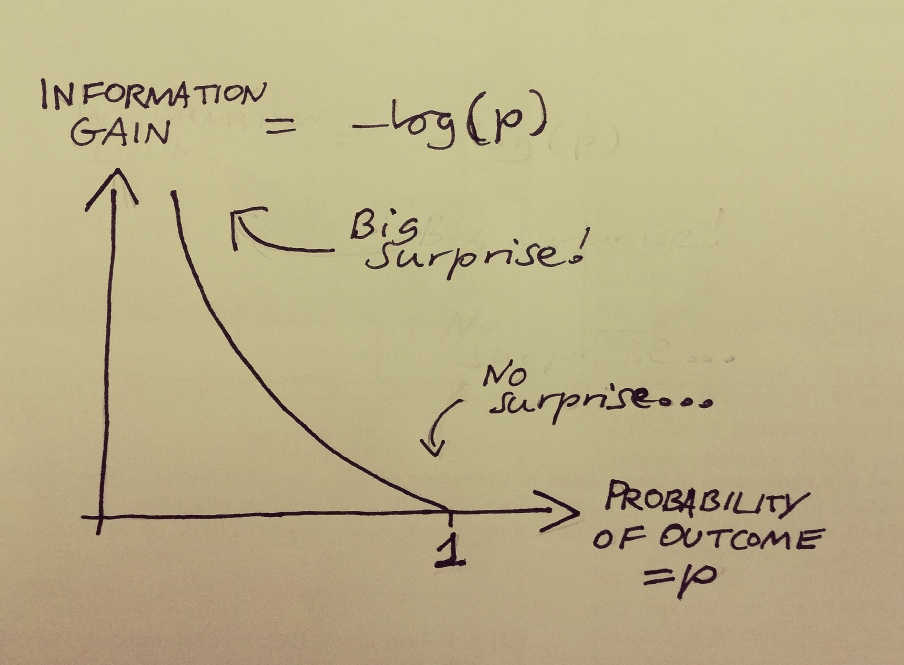
Figure 1: Information gain = -log(p). log is the natural logarithm, and the only important thing is that log(p)=0 when p=1, and it increases as p falls.

You may think: this is a bit of a complicated function, why does it need to be this one specifically? Why not some other function that increases as surprise grows? I’ll get to that in a bit.

Average Surprise

Now let’s think about what the average expected information gain is, i.e., how much information we expect to gain from an experiment before we do it. This would just be the average information gain of each of the outcomes. To get the average of a thing, just add up all the information gains of each outcome and multiply them by the probability of that outcome:

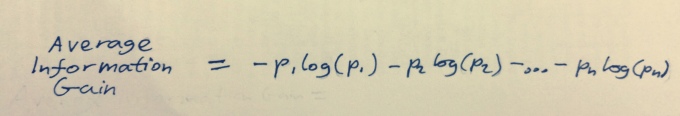
Figure 2: Equation for average information gain.

What we’re talking about here is how much information we have before and after the experiment. Before, we’re relying on some model of how we expect the coin to behave, containing a bunch of assumptions, or approximations. The probabilities in the above equation comes from this model. After, we know everything about the outcome, no approximation or assumptions needed. After the experiment, we have all the information possible, in other words, our description has zero missing information.

So the information gain here is really telling us how much information is missing from our initial model. The equation above tells us how much information is missing from a model, it is in fact the equation for the Shannon entropy of a model predicting probabilities p₁,p₂,…:

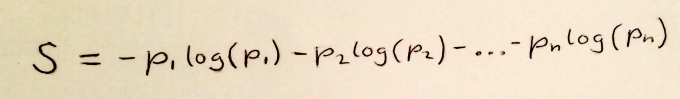
Figure 3: Shannon Entropy!

This is the most general definition of entropy. Claude Shannon came up with this not when he was working on physics, but when studying how to transmit the maximum amount of information in a signal with the smallest number of bits.

He showed, with his famous source coding theorem, that the Shannon entropy of a model is technically the number of bits of information you gain by doing an experiment on a system your model describes. This is the reason you need to describe information gain with specifically a log function – the source coding theorem doesn’t work otherwise. This excellent set of lectures by David MacKay goes more into this stuff.

Now that we have our definition of entropy, let’s think about what it means in terms of flipping coins. In the case of the joke coin with p_heads=1 and p_tails=0, there’s no scope for information gain with an experiment, so one would expect our model of probabilities to have zero entropy. Plug p_heads and p_tails into the equation in figure 3, and you’ll find it to be zero. For the weighted coin, p_heads=0.1, p_tails=0.9, plugging these into the equation we find it has some non-zero entropy, since we can gain some information from flipping the coin. For the fair coin, p_heads=0.5, p_tails=0.5, plugging this into the equation we get a larger number for the weighted coin, since we know less about this coin. We can’t even make a statement about which outcome is more likely.

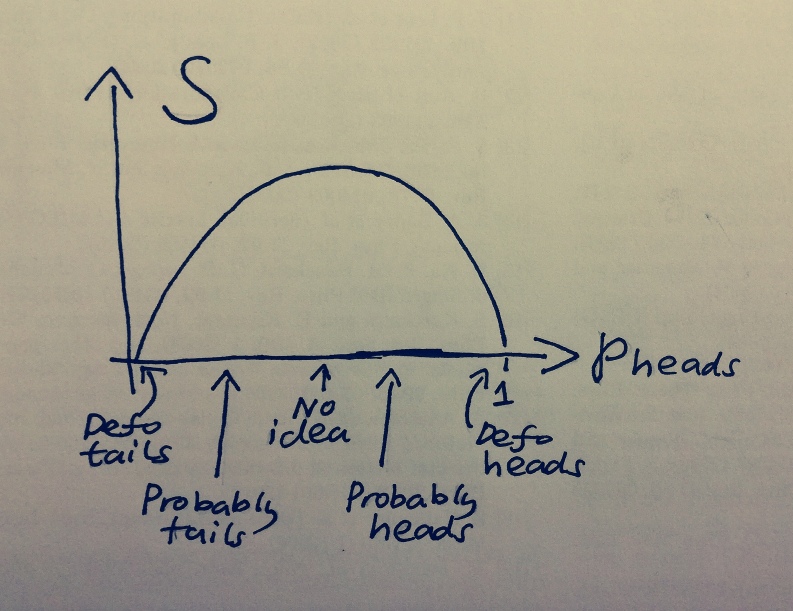
Figure 4: S for different predictions of the outcome of a coin flip.

Once again, this is all about how we’re describing the coin. Instead of just using these probabilities, we could model the whole thing properly with Newton’s laws, and with knowledge of how strongly the coin was flipped, its initial position, velocity, etc, we could make a precise prediction about the outcome. The entropy of this description would be zero.

Information and the Second Law

Working with this definition, the second law of thermodynamics comes pretty naturally. Imagine we were studying the physics of a cup of coffee. If we had perfect information, and knew the exact positions and velocities of all the particles in the coffee, and exactly how they will evolve in time, then S=0, and would stay at 0. We always know exactly where all the particles are at all times.

However, what if there was a rogue particle we didn’t have information about, then S is small but non-zero. As that particle (possibly) collides with other particles around it, we become less sure what the position and velocity of those neighbours could be. The neighbours may collide with further particles, so we don’t know their velocities either. The uncertainty would spread like a virus, and S can only increase. It can never go the other way.

Here is a tasty aside. The second law defines an arrow of time, making the future look different to the past. You may argue that the above argument can be repeated going in the reverse direction in time, then entropy would increase as you go backwards. The reason this isn’t the case isn’t actually well understood, but it probably has something to do with the big bang. Do a read of this to learn more.

So I’ve said that this S is about a description, rather than a physical quantity. But entropy is usually considered to be a property of the stuff we’re studying. What’s going on there? This brings us to…

2: Boltzmann: Microstates and Macrostates

In physics, we can separate models into two broad groups. The first, with “perfect” information, is aiming to produce exact predictions. This is the realm containing, for example, Newton’s laws. The specification of a “state” in one of these models contains all possible information about what it’s trying to describe, and is called a microstate.

The second group of models are those with “imperfect information”, containing only some of the story. Included in the second set is thermodynamics. Thermodynamics seeks not to describe the positions and velocities of every particle in the coffee, but more coarse quantities like the temperature and total energy, which only give an overall impression of the system. A thermodynamic description is missing any microscopic information about particles and forces between them, so is called a macrostate.

A microstate specifies the position and velocity of all the atoms in the coffee.

A macrostate specifies temperature, pressure on the side of the cup, total energy, volume, and stuff like that.

In general, one macrostate corresponds to many microstates. There are many different ways you could rearrange the atoms in the coffee, and it would still have the same temperature. Each of those configurations of atoms corresponds to a microstate, but they all represent a single macrostate.

Some macrostates are “bigger” than others, containing lots of microstates, and some contain little. We can loosely refer to the number of ways you could rearrange the atoms while remaining in a macrostate as its size.

Entropy of  a Macrostate

What does all this have to do with entropy? If I were to tell you that your coffee is in a certain microstate, you would have all the information there is to have about the coffee. If I instead told you what macrostate it was in, this gives you some information, but not all.

The information I gave you narrows down the set of possible microstates the coffee could be in. But you still don’t know for sure exactly what’s going on in the coffee, so there is missing information and a non-zero entropy. But if the coffee was in a macrostate corresponding to less microstates, our description would give more information, since we then narrowed down further the number of microstates the coffee could be in. Our description contains more information, so this is a lower entropy macrostate.

We are now in a position where we can define the entropy of a macrostate, a macroscopic description of a system. It is a function of the number of microstates, that becomes zero when there is only one microstate (since then we know everything), and goes up as microstates increase. The answer: the entropy of a macrostate is the logarithm of the number of microstates it contains.

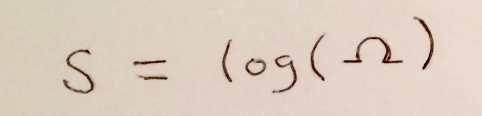
Figure 5: Boltzmann entropy! Ω denotes the number of microstates you can be in while still being in the specified macrostate.

This is called the Boltzmann entropy, and it’s what people are usually referring to when they talk about entropy in a physics context.

For messy thermodynamic systems like the coffee, entropy is a measure of how many different ways you can rearrange its constituents without changing its macroscopic behaviour. The Boltzmann entropy can be derived from the Shannon entropy. It is not a different definition, but a special case of the Shannon entropy, the case where we’re interested only in macroscopic physics.

The Second Law for Macrostates

Working with this definition, the second law of thermodynamics comes pretty naturally. Over time, a hot and messy system like a cup of coffee will explore through microstates randomly, the molecules will move around producing different arrangements. Without any knowledge of what’s going on with the individual atoms, we can only assume that each microstate is equally likely. What macrostate is the system most likely to end up in? The one containing the most microstates. Which is also the one of highest entropy.

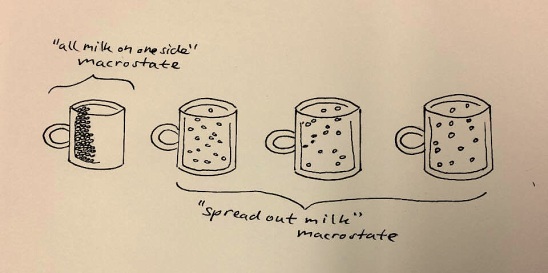
Consider the milk in your coffee. Soon after adding the milk, it ended up evenly spread out through the coffee, since the macrostate of ‘evenly spread out milk’ is the biggest, containing the most microstates. So it has the highest entropy. There are many different ways the molecules in the milk could arrange themselves while conspiring to present a macroscopic air of spreadoutedness.

You don’t expect all the milk to suddenly pool up into one side of your cup, since this would be a state of low entropy. There are few ways the milk molecules could configure themselves while making sure they all stayed on that side. The second law predicts that you will basically never see your coffee naturally partition like this.

Figure 6: Cups of coffee in different microstates. The little blobs represent molecules of milk.

3: Clausius: The Mystery Function of Thermodynamics

When one talks about the Boltzmann entropy, naturally there is a transition between considering entropy a property of the description to a property of physics. Different states in thermodynamics (macrostates) can be assigned different entropies depending on how many microstates it represents.

Once we stop thinking at all about what is going on with individual atoms, we are left with a somewhat mysterious quantity, S.

The “original” entropy, now known as the thermodynamic entropy, is a property of a system related to its temperature and energy. This was defined by Clausius in 1854, before the nature of the atoms at the macroscopic level were understood. Back then, not everyone had been convinced that atoms or molecules were even a thing.

The thermodynamic entropy is the same quantity as the Boltzmann entropy, but was defined in terms of it’s relation to other thermodynamic quantities. Here is the definition:

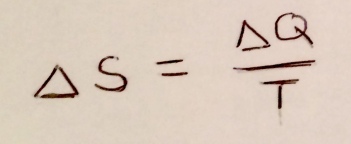
Figure 7: Thermodynamic entropy!

In words, it says that when ΔQ of heat energy is added to a system, the change in entropy ΔS, will be equal to ΔQ divided by temperature T.

This isn’t a very illuminating equation. I’ll try to at least loosely connect it to information and all that stuff. Imagine again pouring a drop of milk into your coffee. If, by some twist of fate, the cup was instantly cooled until both the milk and coffee froze, the milk would be frozen into the pretty pattern it made when it hit the coffee. This is quite a special, low entropy (small number of microstates) macrostate.

You’re annoyed by the sudden freezing of your tea so you shove it in the microwave to add ΔQ worth of heat. As it melts, the milk is allowed to mix more and more with the tea, heading towards states of higher mixedness, ΔQ leads to ΔS. The division by T? As it approaches a state one would happily drink (T getting larger), adding more ΔQ leads to less of an increase in S. The milk is close to being fully mixed in, heating it more has less of an effect on S. A bit of a law of diminishing returns situation there.

Bonus Physics!

So there you are, that’s my little tour of entropy. I hope you are feeling suitably confused. Good, that makes me feel smart. I have one more nice idea to give you that I think ties all the above discussions together quite nicely.

There’s this thing in computer science called Landauer’s principle. It tells you about the theoretical minimum amount of energy a logic gate in a computer takes up. A simple example of a logic gate is an AND gate:

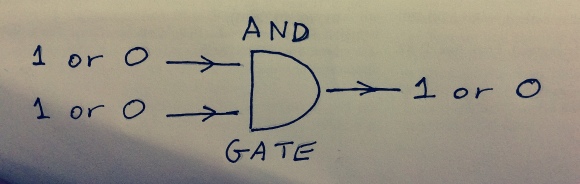
Figure 7: An AND gate. It has two electrical wires going in, and one going out. This particular logic gate only returns “1” if both of the inputs are “1”, and “0” otherwise.

An AND gate takes in two bits of information. The first input can either be on or off, electrical pulse or no electrical pulse (which we can represent with a 1 or a 0). And the same for the second input. The gate gives out only one bit of information, it only has one output that can give out either 1 or 0. So AND gates destroy information. By information in this case, I mean information that could be printed on a screen of the computer the AND gate lives in. If you do the calculation, every time the AND gate does it’s operation, the computer’s Shannon entropy increases by log2.

Now let’s think about energy. Logic gates use up energy due to dissipation of heat, what I was calling ΔQ from before. We know from before that this is related to entropy via the equation for thermodynamic entropy. Thermodynamic entropy is the same as the Shannon entropy in this case, which is log2, so the minimum amount of energy a logic gate can use up is temperature times log2. Kind of neat!

Ok this is now properly the end. Except for this: there is a lot of interesting things black holes do relating to entropy and information. I wrote a post all about that, and you can read that thing if you click here.

Ok thanks bye.

Why entropy is at the heart of information theory

All of thermodynamics can be derived from entropy

More on the arrow of time

Reversible computing: logic gates that don’t destroy information